Функция котангенс в excel
Тригонометрия в Excel: основные функции
Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.
Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121) , и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.
Еще одна функция – ПИ() , не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.
Радианы в градусы и градусы в радианы
Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:
- ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
- РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.
Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.
Прямые тригонометрические функции
Конечно, Вы знаете эти функции:
- COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
- SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе
Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».
Производные тригонометрические функции
Еще две функции Вам так же знакомы – это тангенс и котангенс:
- TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
- COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.
Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.
Другие тригонометрические функции
Среди прочих тригонометрических функций можно выделить секанс и косеканс:
- SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
- CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету
Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.
Обратные тригонометрические функции
Такие функции выполняют обратный расчет по отношению к перечисленным выше:
- Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса) .
- Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса) .
- Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса) .
- Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).
Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ .
Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.
Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!
Как в excel сделать котангенс?
 Дата: 23 сентября 2016 Категория: Excel Поделиться, добавить в закладки или статью
Дата: 23 сентября 2016 Категория: Excel Поделиться, добавить в закладки или статью
Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.
Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121), и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.
Еще одна функция – ПИ(), не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.
Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:
- ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
- РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.
Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.
Конечно, Вы знаете эти функции:
- COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
- SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе
Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».
Еще две функции Вам так же знакомы – это тангенс и котангенс:
- TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
- COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.
Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.
Среди прочих тригонометрических функций можно выделить секанс и косеканс:
- SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
- CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету
Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.
Такие функции выполняют обратный расчет по отношению к перечисленным выше:
- Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса).
- Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса).
- Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса).
- Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).
Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ.
Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.
Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!
Поделиться, добавить в закладки или статью
Котангенс excel
В разделе Естественные науки на вопрос Как в MS Excel можно вычислить котангенса угла? заданный автором Особняк лучший ответ это По-моему примерно так:
Угол (ы) в градусах.
22 ответа
Привет! Вот подборка тем с ответами на Ваш вопрос: Как в MS Excel можно вычислить котангенса угла?
Как Брадис высчитывал значения для своей знаменитой таблицы?
Тригонометрия Чему равен арктангенс (- 1/2) люди…как найти синус, косинус и катангенс, если известен тангенс?
Ответ от Простреливать
Пишешь в ячейке формулу : «=1/TAN(x)», где х-угол в радианах.Самой формулы котангенса в Excel нету
Ответ от шеврон
Например чтобы найти котангенс под углом 30 градусов, используйте следующую формулу:
=1/TAN(30*PI()/180)
Как в MS Excel можно вычислить котангенса угла?
Войдите что бы оставлять комментарии
По-моему примерно так: Угол (ы) в градусах.



ответ написан 8месяцев назад
Войдите что бы оставлять комментарии
Пишешь в ячейке формулу : «=1/TAN(x)», где х-угол в радианах. Самой формулы котангенса в Excel нету
ответ написан 8месяцев назад
Войдите что бы оставлять комментарии
Например чтобы найти котангенс под углом 30 градусов, используйте следующую формулу: =1/TAN(30*PI()/180)
Математические и тригонометрические функции (справочник)
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
Возвращает модуль (абсолютную величину) числа.
Возвращает арккосинус числа.
Возвращает гиперболический арккосинус числа.
ACOT

Возвращает арккотангенс числа.
ACOTH

Возвращает гиперболический арккотангенс числа.
Возвращает агрегат для списка или базы данных.
АРАБСКОЕ

Преобразует римские числа в арабские в виде числа.
Возвращает арксинус числа.
Возвращает гиперболический арксинус числа.
Возвращает арктангенс числа.
Возвращает арктангенс для заданных координат x и y.
Возвращает гиперболический арктангенс числа.
ОСНОВАНИЕ

Преобразует число в текстовое представление с данным основанием (базой).
Округляет число до ближайшего целого или кратного.
ОКРВВЕРХ.МАТ

Округляет число в большую сторону до ближайшего целого или кратного.
Округляет число до ближайшего целого или кратного. Число округляется до большего значения вне зависимости от его знака.
Возвращает количество комбинаций для заданного числа объектов.
ЧИСЛКОМБА

Возвращает количество комбинаций с повторами для заданного числа элементов.
Возвращает косинус числа.
Возвращает гиперболический косинус числа.
COT

Возвращает котангенс угла.
COTH

Возвращает гиперболический котангенс числа.
CSC

Возвращает косеканс угла.
CSCH

Возвращает гиперболический косеканс угла.
ДЕС

Преобразует текстовое представление числа в заданном основании в десятичное число.
Преобразует радианы в градусы.
Округляет число до ближайшего четного целого.
Возвращает число e, возведенное в указанную степень.
Возвращает факториал числа.
Возвращает двойной факториал числа.
Округляет число до ближайшего меньшего по модулю значения.
ОКРВНИЗ.МАТ

Округляет число в меньшую сторону до ближайшего целого или кратного.
Округляет число в меньшую до ближайшего целого или до ближайшего кратного для точности. Число округляется в меньшую сторону независимо от знака.
Возвращает наибольший общий делитель.
Округляет число до ближайшего меньшего целого.
ISO.ОКРВВЕРХ

Округляет число в большую сторону до ближайшего целого или кратного.
Возвращает наименьшее общее кратное.
Возвращает натуральный логарифм числа.
Возвращает логарифм числа по заданному основанию.
Возвращает десятичный логарифм числа.
Возвращает определитель матрицы массива.
Возвращает обратную матрицу массива.
Возвращает матричное произведение двух массивов.
Возвращает остаток от деления.
Возвращает число, округленное с требуемой точностью.
Возвращает мультиномиальный коэффициент множества чисел.
МЕДИН

Возвращает матрицу единицы или заданный размер.
Округляет число до ближайшего нечетного целого.
Возвращает число пи.
Возвращает результат возведения числа в степень.
Возвращает произведение аргументов.
Возвращает целую часть частного при делении.
Преобразует градусы в радианы.
Возвращает случайное число в интервале от 0 до 1.
Возвращает массив случайных чисел от 0 до 1. Однако вы можете указать количество строк и столбцов для заполнения, минимального и максимального значений, а также возвращать целые числа или десятичные значения.
Возвращает случайное число в интервале между двумя заданными числами.
Преобразует арабские числа в римские в виде текста.
Округляет число до указанного количества десятичных разрядов.
Округляет число до ближайшего меньшего по модулю значения.
Округляет число до ближайшего большего по модулю значения.
SEC

Возвращает секанс угла.
SECH

Возвращает гиперболический секанс угла.
Возвращает сумму степенного ряда, вычисленную по формуле.
Возвращает знак числа.
Возвращает синус заданного угла.
Возвращает гиперболический синус числа.
Возвращает положительное значение квадратного корня.
Возвращает квадратный корень из значения выражения (число * пи).
Возвращает промежуточный итог в списке или базе данных.
Суммирует ячейки, удовлетворяющие заданному условию.
Суммирует ячейки в диапазоне, удовлетворяющие нескольким условиям.
Возвращает сумму произведений соответствующих элементов массивов.
Возвращает сумму квадратов аргументов.
Возвращает сумму разностей квадратов соответствующих значений в двух массивах.
Возвращает сумму сумм квадратов соответствующих элементов двух массивов.
Возвращает сумму квадратов разностей соответствующих значений в двух массивах.
Возвращает тангенс числа.
Возвращает гиперболический тангенс числа.
Отбрасывает дробную часть числа.
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Примечание: Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Была ли информация полезной? Для удобства также приводим ссылку на оригинал (на английском языке).
Тригонометрическая функция: Котангенс угла (ctg)
Определение
Котангенс острого угла α (ctg α или cotan α) – это отношение прилежащего катета (b) к противолежащему (a) в прямоугольном треугольнике.

Например:
a = 3
b = 4
ctg α = b / a = 4 / 3 ≈ 1,334.
График котангенса
Функция котангенса пишется как y = ctg (x) . График в общем виде выглядит следующим образом ( x ≠ nπ, –∞ ):

Свойства котангенса
Ниже в табличном виде представлены основные свойства котангенса с формулами.
| Свойство | Формула |
| Четность/симметричность | ctg (-α) = -ctg α » data-order=» ctg (-α) = -ctg α » > ctg (-α) = -ctg α |
| Четность/симметричность | ctg (90°- α) = tg α » data-order=» ctg (90°- α) = tg α » > ctg (90°- α) = tg α |
| Тригонометрические тождества | ctg α = cos α / sin α » data-order=» ctg α = cos α / sin α » > ctg α = cos α / sin α |
| ctg α = 1 / tg α » data-order=» ctg α = 1 / tg α » > ctg α = 1 / tg α | |
| Котангенс двойного угла | ctg 2α = (ctg 2 α — 1) / 2 ctg α » data-order=» ctg 2α = (ctg 2 α — 1) / 2 ctg α » > ctg 2α = (ctg 2 α — 1) / 2 ctg α |
| Котангенс суммы углов | ctg (α+β) = (ctg α ctg β — 1) / (ctg β + ctg α) » data-order=» ctg (α+β) = (ctg α ctg β — 1) / (ctg β + ctg α) » > ctg (α+β) = (ctg α ctg β — 1) / (ctg β + ctg α) |
| Котангенс разности углов | ctg (α-β) = (ctg α ctg β + 1) / (ctg β — ctg α) » data-order=» ctg (α-β) = (ctg α ctg β + 1) / (ctg β — ctg α) » > ctg (α-β) = (ctg α ctg β + 1) / (ctg β — ctg α) |
| Сумма котангенсов |  |
| Разность котангенсов |  |
| Произведение котангенсов | ctg α ctg β = (ctg α + ctg β) / (tg α + tg β) » data-order=» ctg α ctg β = (ctg α + ctg β) / (tg α + tg β) » > ctg α ctg β = (ctg α + ctg β) / (tg α + tg β) |
 | |
| Проивезедение котангенса и тангенса | tg α ctg β = (tg α + ctg β) / (ctg α + tg β) » data-order=» tg α ctg β = (tg α + ctg β) / (ctg α + tg β) » > tg α ctg β = (tg α + ctg β) / (ctg α + tg β) |
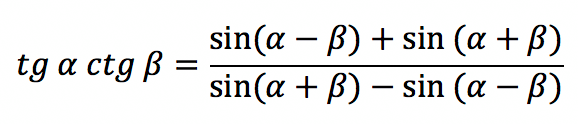 | |
| Производная котангенса | ctg’ x = 1 / sin 2 (x) » data-order=» ctg’ x = 1 / sin 2 (x) » > ctg’ x = 1 / sin 2 (x) |
| Интеграл котангенса | ∫ ctg x dx = ln |sin x| + C » data-order=» ∫ ctg x dx = ln |sin x| + C » > ∫ ctg x dx = ln |sin x| + C |
| Формула Эйлера | ctg x = i(e ix + e —ix ) / (e ix — e —ix ) » data-order=» ctg x = i(e ix + e —ix ) / (e ix — e —ix ) » > ctg x = i(e ix + e —ix ) / (e ix — e —ix ) |
Обратная к котангенсу функция
Если котангенс угла у равняется х (c tg y = x ), значит арккотангенс x равен у :



